We all know what decimal numbers are: 1, 2, 3, 4, 5, etc. However, many other numeral systems exist and you might have heard about or seen others, like hexadecimal numbers (for example: 3F2B) or
binary numbers (for example: 10101011), which may seem cryptic and meaningless.
These hexadecimal or binary numbers can easily be converted to the well-known decimal numbers. So, why do these other systems exist and why do we need them even though the “normal” decimal numbers (1, 0, 9, 2 etc.)
can be used for everything you can think of?

Other numeral systems exist because there are specific uses where a certain numeral system is easier to use and offers advantages over another.

• Our most common numeral system is the decimal (or “base 10”) system. It has 10 numerals (0-9), which can be used to describe any possible number that we use daily. It is very convenient for counting and calculations,
  plus it is the most intuitive.
• Another numeral system is the hexadecimal (or “base 16”) system. It has 16 numerals (0-9 and A-F). It is very convenient to describe the value of bytes used in computer science.
• The third numeral system is the binary (or “base 2”) system. It has 2 numerals
  (0 and 1), and it is used to represent the value of bits – the type of information stored in a computer’s memory. It has various advantages in electronics, and it also offers certain mathematical advantages.

Binary and hexadecimal numbers are widely used in computer science. For this article, we’ll focus on binary numbers. Binary numbers can be considered the very basic representation of a number in an electronic device.
They represent an ON state (1) and OFF state (0). Many of these ON and OFF states represent a decimal number, for example:

Binary	Decimal
0001	1
0010	2
0011	3
1000	8

Converting to and from a decimal will be covered in another article. For now, we will answer why computers use the binary (“base 2”) number system and why electronic devices store binary numbers.
This will help to explain why binary numbers are so important. The very first computers used binary numbers, and they are still used today.

Binary in Electronics

Every computer is made up of many electronic components. That is why a basic knowledge of electronics is needed to understand how and why binary numbers are used in computers. We’ll keep it very simple.

A computer is built with many connections and components, which are used to transfer and store data, as well as communicate with other components. Most of that storing, transferring, and communicating
happens with digital electronics. Digital electronics use the binary system (ON/OFF). A signal with a series of ON/OFF pulses is equal to a binary number.

In electronics, a voltage level or current flow is a way to represent a value. For example, 5V (volts) or 0.5A (amperes). The makers of electronic devices could, of course, assign any meaning that they want
to different voltage values. If you need 10 values, you could divide the range of 0V-4V (including 0, which creates 5 “steps”) by 10. You would end up with 0.5V per step:

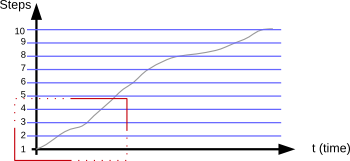
V	Step
0.0	1
0.5	2
1.0	3
1.5	4
2.0	5
…	…

However, the higher the voltage or current flow, the higher the energy consumption of a device.

Do you see the problem here?

Well, the higher the voltage or current flow, the higher the energy consumption of a device.

This means that when building an electronic device, it is most often desired to have the energy consumption as low as possible and to have a low voltage. Furthermore, electronic signals are not always steady
and can vary because of surrounding influences, like nearby internal circuits for other electronic devices.

Using the 0.5V per step from the previous example, we assume that electronic circuits could interfere with the voltage levels and make them appear 0.25V higher or lower (this is an arbitrary example).
This might then lead to voltage levels where it gets difficult to distinguish which value it represents. The voltage 0.5 could either mean 1, 2, or 3 since there is the possibility of it falling into the range of 0.25V to 0.75V.

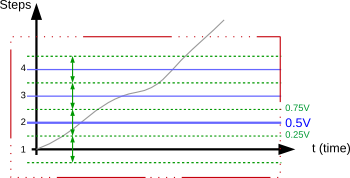
V	Min.	Max.	Step
0.0	-0.25	0.25	1
0.5	0.25	0.75	2
1.0	0.75	1.25	3
1.5	1.25	1.75	4
…	…	…	…

As a result, we cannot divide the 5V into 10 steps. The values could be misinterpreted. A computer might suddenly make wrong calculations because of random interference.

This example of voltage ranges shows that it is necessary to have a safe range between two voltage levels in order to read the correct value with 100 percent probability. (There are additional methods on the software level
to verify that data is read correctly, but this is out of the scope of this article). This is one of the reasons why the binary system – using only two levels/states – is used in computers. Binary comes from the Latin
language and means that something is composed of two things. Binary electronics are usually called digital electronics.

Another major reason is because a lot more circuitry is needed to distinguish between more than two voltage levels. Each additional state needs about the same amount of additional circuitry. For example, for a binary system,
2*n is needed (n=circuitry size). For a three-state system, 3*n is needed. And so on.

There are two reasons computers use the binary system

• Two clearly distinct states provide a safety range for reliability.
• Least amount of necessary circuitry, which results in the least amount of space, energy consumption, and cost.

Quantum computing, however, might one day replace the binary system. It might be the next big step in how our computers work!