A binary number with 8 bits (1 byte) can represent a decimal value in the range from 0 – 255. However, this only includes whole numbers and no real numbers (e.g. fractions) like 0.5 or 20.456 etc.
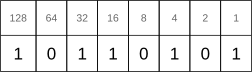
To represent all real numbers in binary form, many more bits and a well defined format is needed. This is where floating point numbers are used. However, floating point is only a way to approximate a real number. Imagine the number PI 3.14159265… which never ends. It would need an infinite number of bits to represent this number. A binary floating point number is a compromise between precision and range. Depending on the use, there are different sizes of binary floating point numbers.
Why is it called “floating point”?
As the name suggests, the point (decimal point) can float. The floating point format uses the scientific notation which is a form of writing numbers which are too big or too small to conveniently write in decimal form. The base 10 scientific notation is x*10y and it allows the decimal point to be moved around.
The number 523.0 for example can be written in scientific notation as 523.0*100, 52.30*101 or 5.230*102. This example shows the “floating” decimal point which appears on different positions in the number x depending on the exponent y. Moving the decimal point one location to the right increases the exponent, moving it to the left decreases the exponent.
Floating point in binary
The two most common floating point storage formats are defined by the IEEE 754 standard (Institute of Electrical and Electronics Engineers, a large organization that defines standards) and are:
- short real: 32 bit (also called single precision)
- 1 bit sign, 8 bits exponent, 23 bits mantissa
- long real: 64 bit (also called double precision)
- 1 bit sign, 11 bits exponent, 52 bits mantissa
The following image shows a 32 bit floating point number in binary form. It highlights the parts of the sign “S”, the exponent, and the mantissa.

Here is an example of a floating point number with its scientific notation +34.890625*104. The sign bit is the plus in the example. The mantissa is 34.890625 and the exponent is 4. Since we are in the decimal system, the base is 10.
Some more information about the bit areas:
- Sign
- One single bit. The sign-bit indicates if a number is negative. Therefore, a 1 indicates that the number is negative, a 0 indicates that the number is positive
- mantissa
- 23 bits (in single precision floating point) can represent 8388608 different values. Sometimes also called the significand.
- Exponent
- 8 bits (single precision floating point) can represent 256 different values. However, to
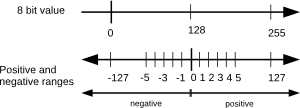
8 bit value with negative and positive range allow positive and negative exponents, half of the range (0-127) is used for negative exponents and the other half (128 – 255) is used for positive exponents. A positive exponent 105 would have a value of 5+127=132. A negative exponent 10-8 would have a value of -8+127=119
- 8 bits (single precision floating point) can represent 256 different values. However, to
Converting a decimal floating point number to binary
Converting a decimal value to binary requires the addition of each bit-position value where

the bit is 1. The decimal value of the binary number 10110101 is 1+4+16+32+128=181 (see picture on the right). When dealing with floating point numbers, the procedure is very similar but some additional steps are required. Converting a decimal floating point number to its binary form is more complicated than the other way around. The conversion to binary is explained first because it shows and explains all parts of a binary floating point number step by step.
A floating point number has an integral part and a fractional part. As example in number 34.890625, the integral part is the number in front of the decimal point (34), the fractional part is the rest after the decimal point (.890625). Here are the steps to convert a decimal number to binary (the steps will be explained in detail after):
- Convert decimal number to binary scientific notation, processing the integral and fractional part independently.
- The scientific binary number is then normalized (the decimal point is moved to the left most position, adjusting the exponent accordingly)
- The exponent is converted to binary
- The binary floating point number is constructed with all converted number parts. The first 1 of the mantissa is omitted.
Step 1
The very first step is to convert the number to binary scientific notation. To convert this floating point value to binary, the integral and fractional part are processed independently.
Converting the integral part to binary:
The integral part is converted like any whole number: 34 is 10 0010 in binary. In the first step, the integral part is divided by 2 (2 because we want to convert to the binary system). Then the whole number part of the result is used to divide by 2 again, and so on until the whole number part reaches 0.
| Calculation | Result | Whole number | Remainder (bit) |
| 34 / 2 | 17 | 17 | 0 |
| 17 / 2 | 8.5 | 8 | 1 |
| 8 / 2 | 4 | 4 | 0 |
| 4 / 2 | 2 | 2 | 0 |
| 2 / 2 | 1 | 1 | 0 |
| 1 / 2 | 0.5 | 0 | 1 |
The resulting bits are calculated in reverse order. Reading the binary number from bottom to top gives us 10 0010 (Hint: writing binary numbers in groups of 4, which is one byte, makes it easier to read them).
Converting the fractional part to binary:
To convert the fractional part, instead of using division as used for the integral part, multiplication is used. If it is a whole number (>= 1.0), the bit is 1. The fractional part of the result is then used for the next calculation. Once the result reaches 1.0, the conversion is finished. However, there are many numbers which do not end up at a 1.0 result. Since there are 23 possible bits for the mantissa (in a single precision floating point number), the conversion ends as soon as 23 bits are reached. The example number with the fractional part .890625 has been chosen on purpose to reach an end of the conversion after only a few calculations.
| Calculation | Result | Whole number | Bit |
| .890625 * 2 | 1.78125 | yes | 1 |
| .78125 * 2 | 1.5625 | yes | 1 |
| .5625 * 2 | 1.125 | yes | 1 |
| .125 * 2 | 0.25 | no | 0 |
| .25 * 2 | 0.5 | no | 0 |
| .5 * 2 | 1 | yes | 1 |
The resulting bits are calculated in the order they are written, which gives us a binary number 111001. The integral and fractional parts of the number 34.890625 combined gives the scientific binary number 100010.111001*20 (34 = 100010 and .890625 = 111001) with the base 2 because it is a binary number (and not a decimal number with the base 10).
Step 2
Normalizing a scientific number means that the decimal point is moved to the left-most possible position by adjusting the exponent accordingly. For the number 100010.111001*20, the decimal point can be moved 5 positions to the left, which increases the exponent by 5: 1.00010111001*25.
Note: As for any scientific notation, the decimal point is always moved to the left-most position so that there is no leading zero. For example, there is no 0.234*102 or 0.365*105. Those numbers would be written as 2.34*101 and 3.65*104. The same rule is used for the binary scientific notation which means that any normalized scientific binary number starts with a 1.
Step 3
The normalization of the binary number resulted in the adjusted exponent of 5. As noted previously, the binary floating point exponent has a negative range and a positive range. Thus, 127 has to be added to the exponent of 5 and then converted to binary: 5+127=132 which is 1000 0100 in binary.
Step 4
Now, the binary floating point number can be constructed. Steps 1 – 3 resulted in:
- the positive number in binary form: 1.00010111001
- the exponent in binary form: 1000 0100
These numbers can now be filled into the bit areas of a 32 bit floating point number.
- Sign
- The number is positive which means the sign is 0
- Mantissa
- The mantissa is 00010111001. Where did the preceding 1 go? As noted in Step 2, any scientific notation ends up with a preceding 1. Therefore, the preceding 1 is omitted since no space has to be wasted for a bit whose state is known.
- Exponent
- The exponent is 1000 0100
The resulting floating point value is 0 10000100 0001011100100000000000:

The converted mantissa value is “left aligned”, which means that any unused bits to the right of the number are filled with 0 to reach the size of the binary number. A double precision 64 bit binary number would have even more bits available which allows for better precision if needed. The converted exponent is “right aligned” and any unused bits to the left of the number are filled with 0.
Converting a binary floating point number to decimal
Converting a binary floating point number to decimal is much simpler than the reverse. For simplicity, we will use the previously converted number again and convert it back to decimal. If everything is done right, the result should be 34.890625.
The binary 32 bit floating point number was: 0 10000100 0001011100100000000000
Again, this is a positive number (the first bit, the sign, is 0), the exponent is 10000100 and the mantissa is 1.00010111001 (omitting any zeros at the end and adding back the omitted 1 in front of the decimal point).
Converting the exponent to decimal:
The conversion is a basic binary to decimal conversion.
22 + 27 = 132
or 4+128=132
Since there is the positive and negative range of +- 127 for exponents (as mentioned earlier), 127 has to be subtracted from the the converted value:
132-127=5
The resulting exponent is 5.
The whole mantissa can now be converted to decimal:
Converting the mantissa does not need the normalization to be undone. The whole number can be calculated as follows:
1.00010111001 * 25
either with negative exponents: (20 + 2-4 + 2-6 + 2-7 + 2-8 + 2-11) * 25 = 34.890625
or fractions: (1 + 1/16 + 1/64 + 1/128 + 1/256 + 1/2048) * 25 = 34.890625
The number is now successfully converted to decimal and the result is 34.890625 which is the decimal representation of the floating point number we started with.

