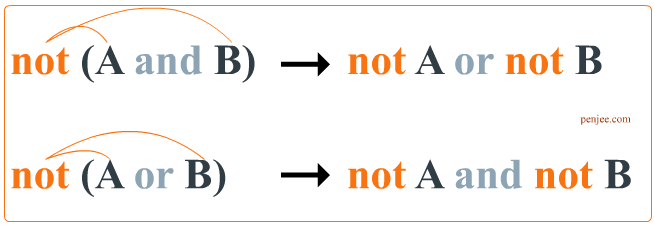Demorgan’s Law is something that any student of programming eventually needs to deal with.

Just tell me the “formula”:

ok the diagram below shows the 2 ways that you can re-write a compound boolean expression using DeMorgan’s Law. (The very bottom of this page shows coding examples and common misconceptions)

---

How do you say “no” to 2 different things?

In real world speech:

It’s Monday, you have an exam on Friday, you might say something like :

   “As long as it is not Friday and I do not know the rules, I will study. ”

Everybody knows what you mean.

But how do we do this in programming? How do we negate 2 boolean expressions?

In Programming:

First, let’s set up a programming problem and look at how we would write the solution code (and then we’ll see how DeMorgan’s law comes into play)

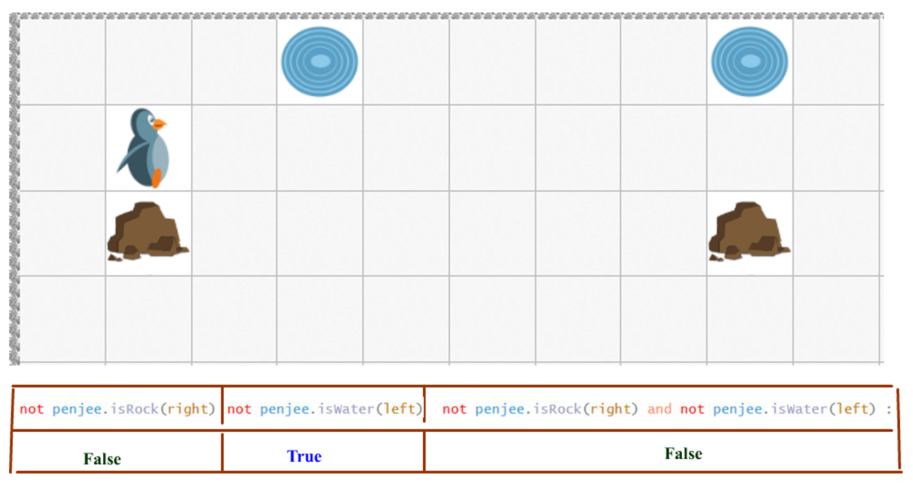
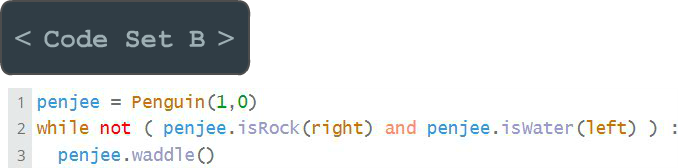
We want to write a loop so that the penguin will   waddle()  to the cell labelled below, that cell between the rock and the water.

The question is… do we want Code Set A or Code Set B  ?

 

Or, maybe it doesn’t matter. Maybe Code Set A and Code Set B will both work .

Spoiler alert – not true . Only 1 of the code sets actually works!

(The answer to this question has a lot to do with DeMorgan’s law )

 

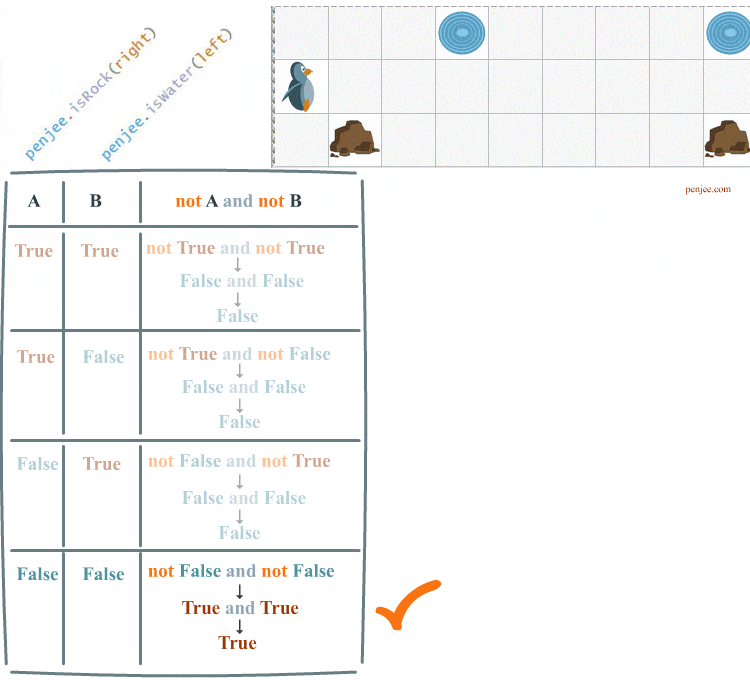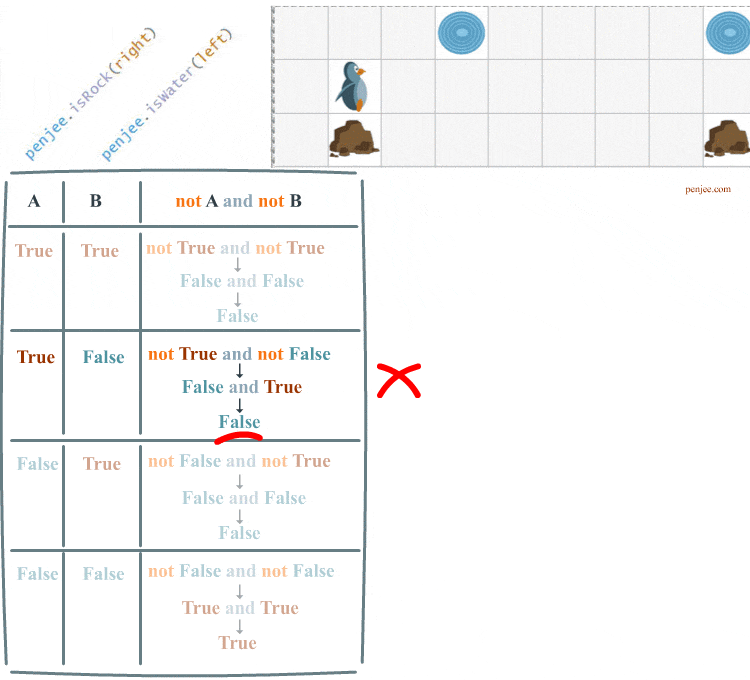
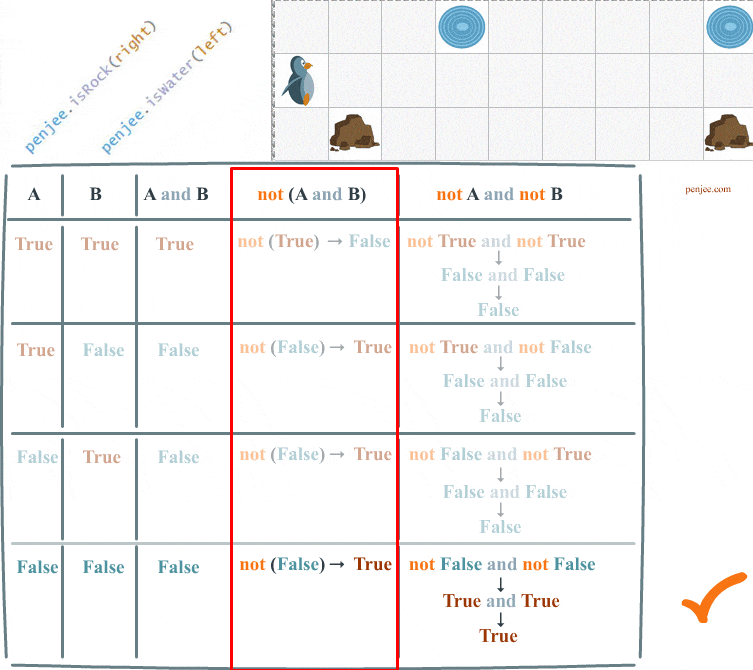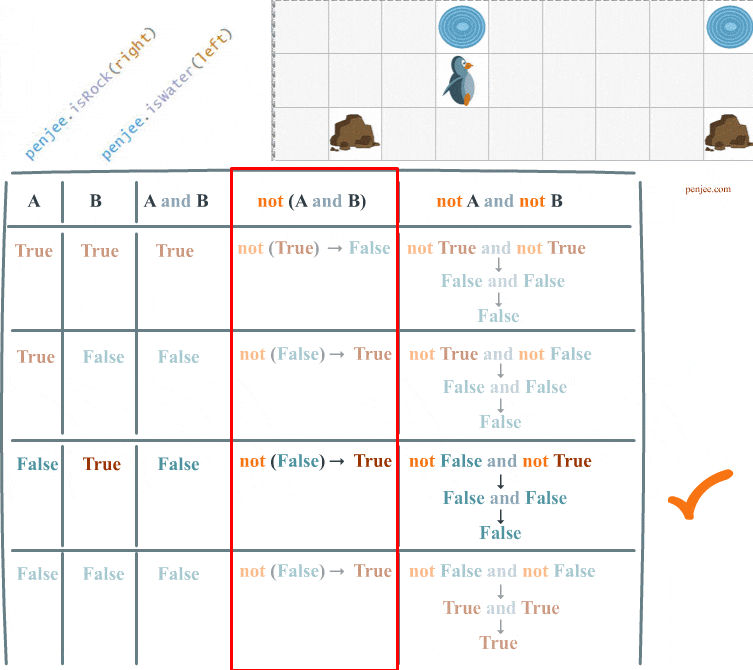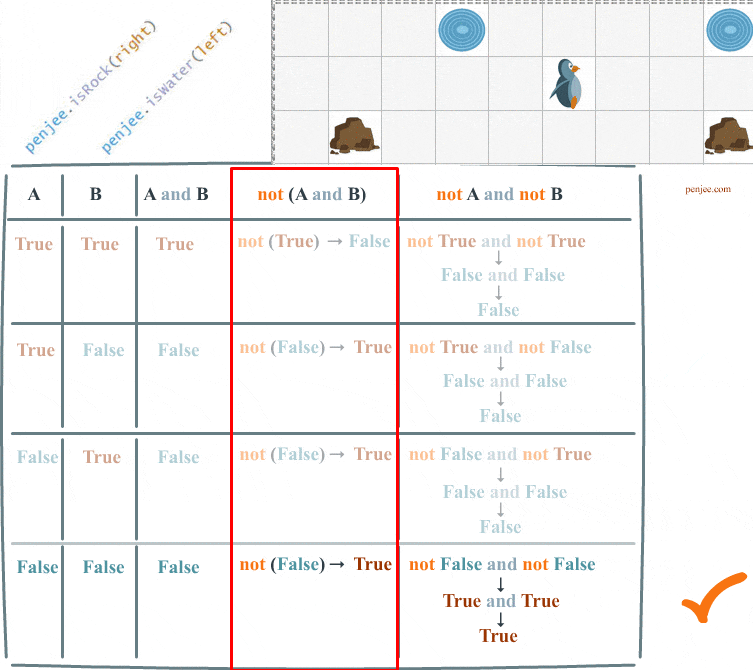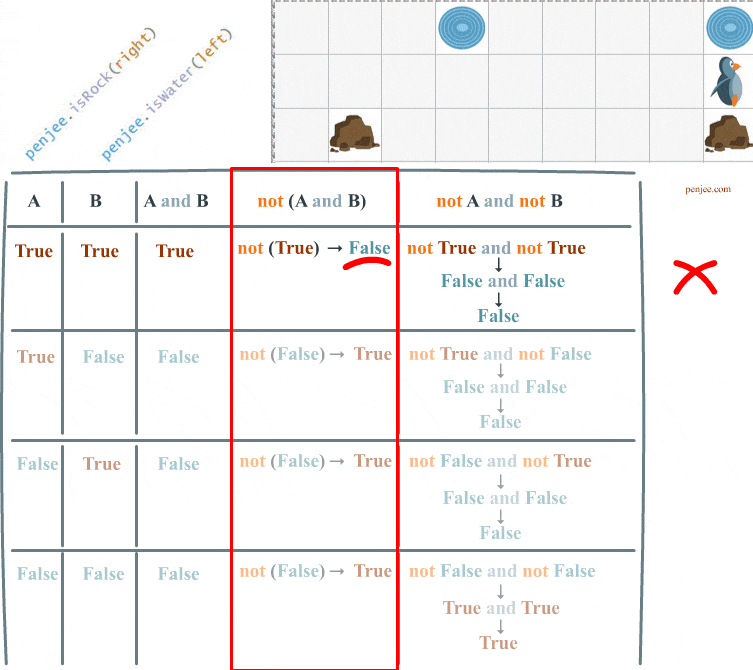
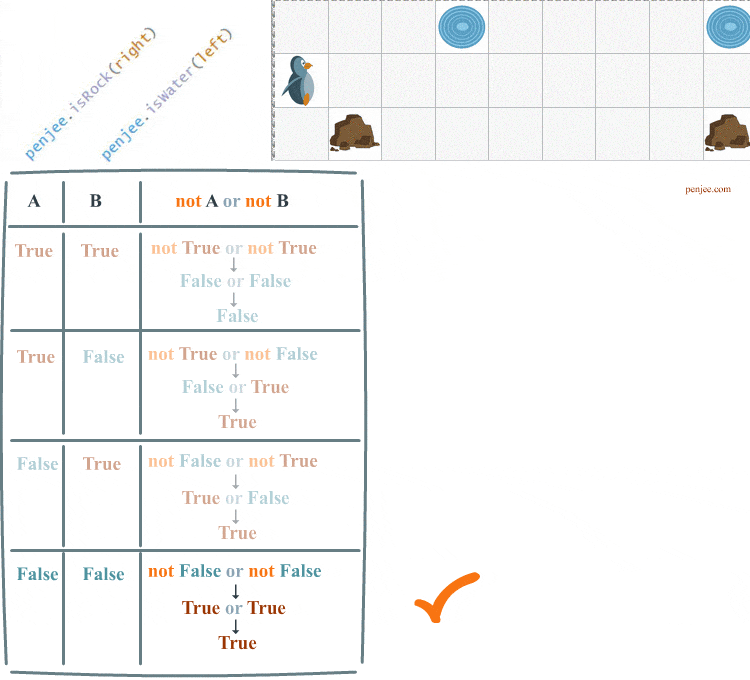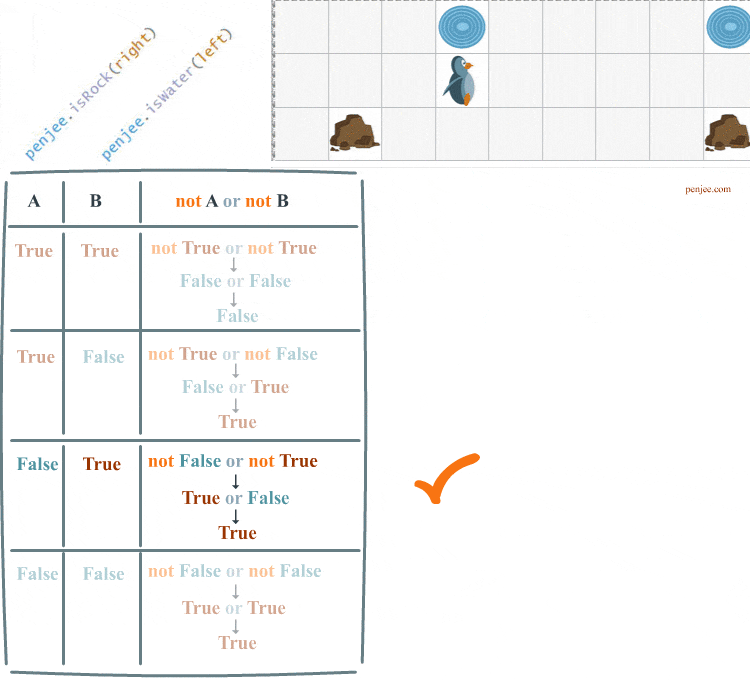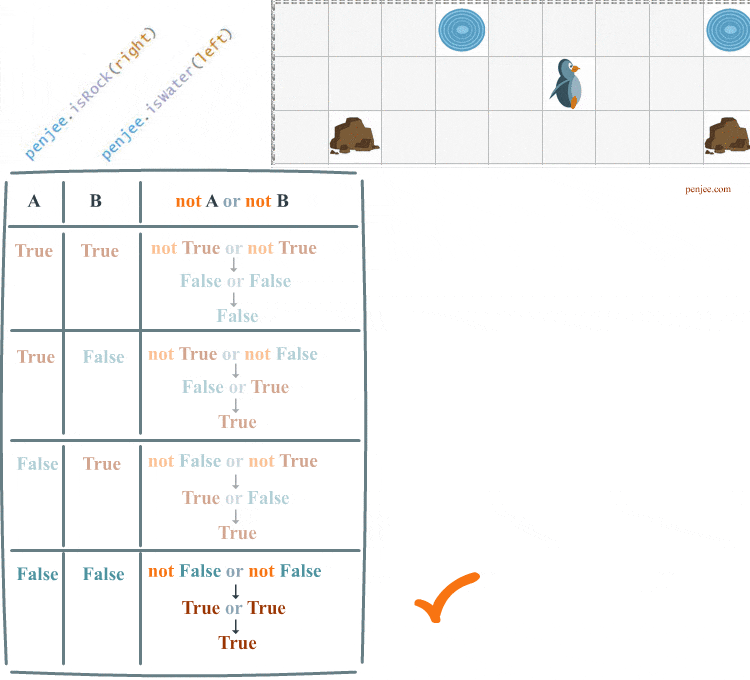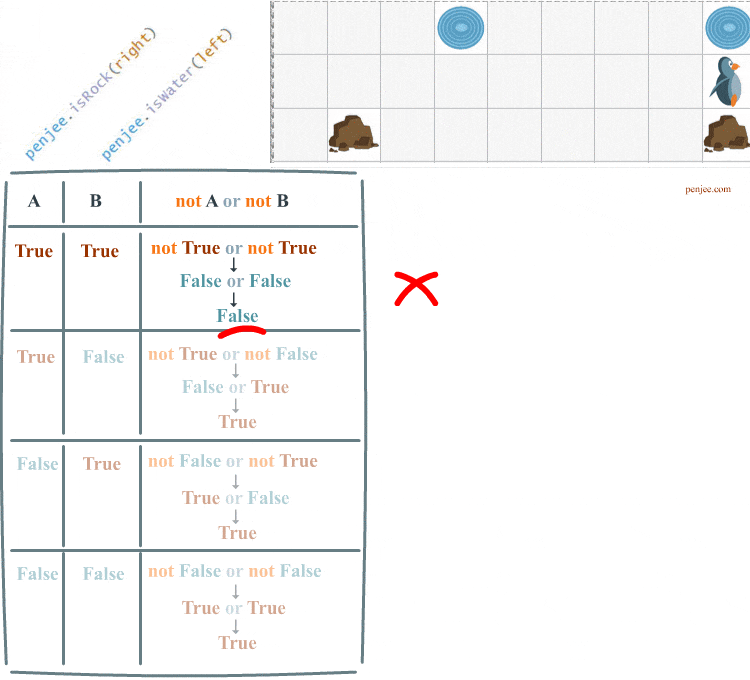
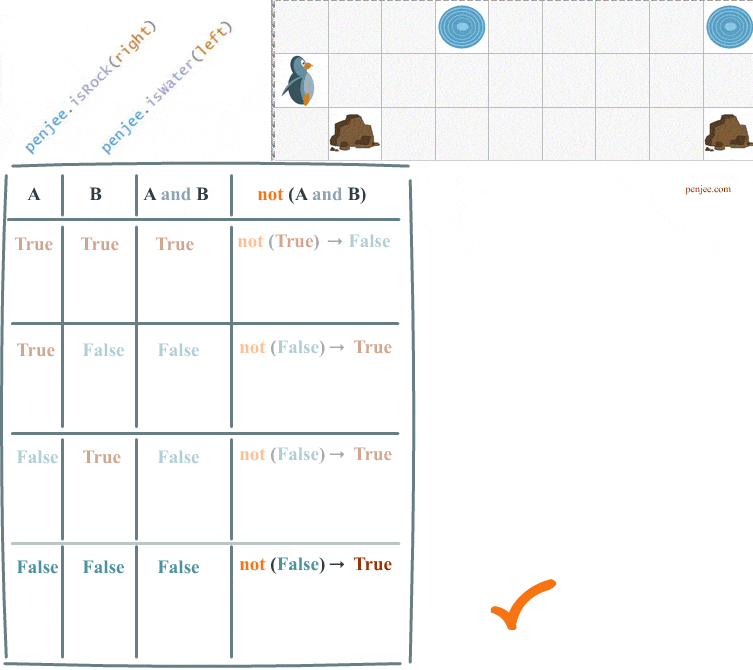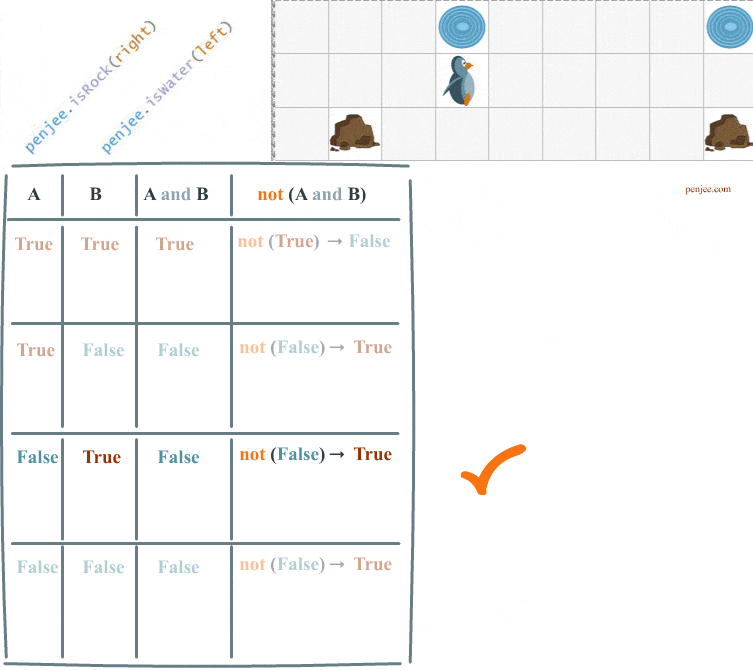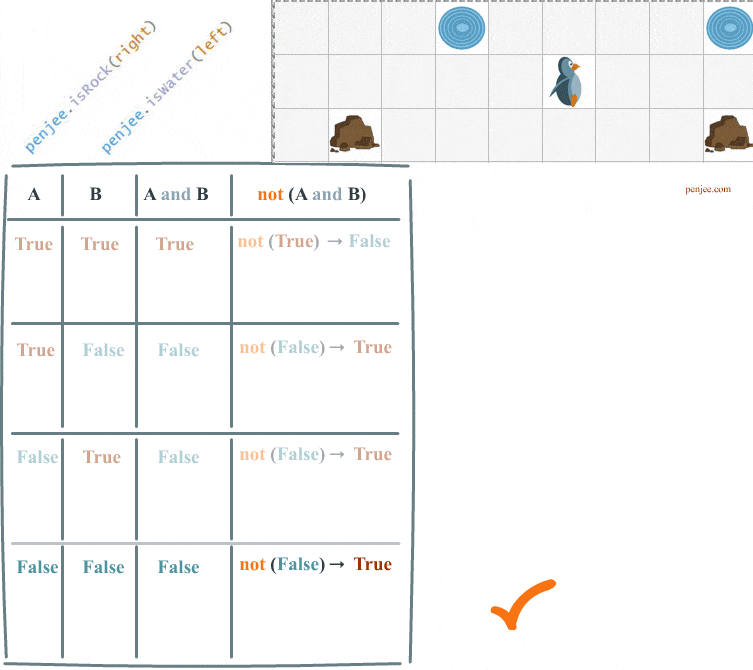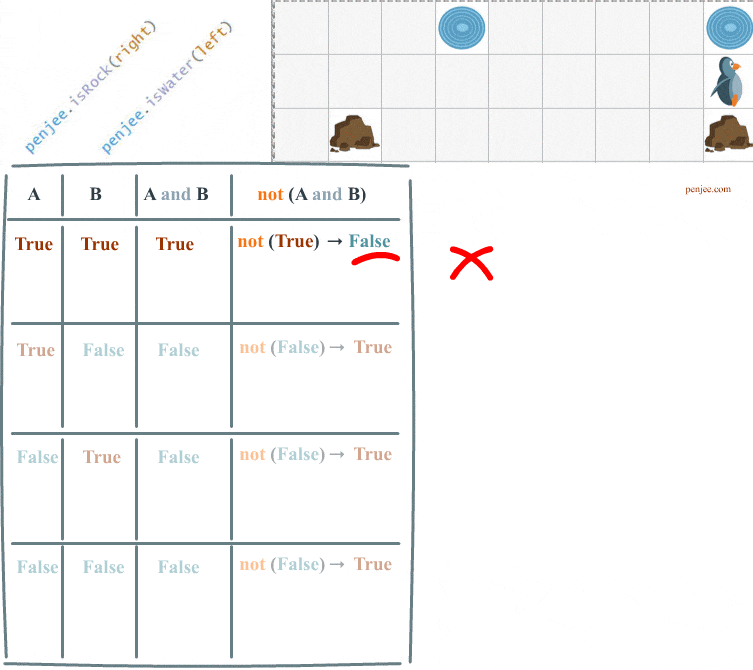
Code Set A and Code Set B can be represented in a truth table. We are going to fill out this truth table over the course of this web page.

Understanding DeMorgan’s law, in programming, is critical if you want to know how to write code that negates 2 boolean conditions. In our code examples, the 2 conditions are penjee.isRock(right)  and penjee.isWater(left) .

And… the answer is … (see animation immediately below)

Animation and Programming Code

 

 

As you can see Code Set A does not achieve our objective. Our penguin only waddles once . Let’s look at the truth table for the case that ends our loop. And then we’ll see what happens when we try to run Code Set B.

The animation below shows both Code Sets A and B .

 

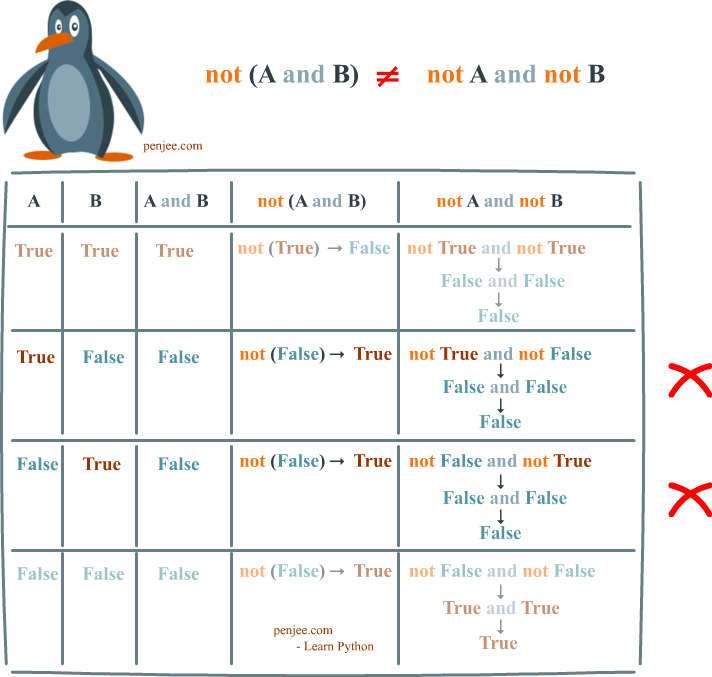
So… from the above examples, we can learn 2 things.

 

First,   not( a and b)  is how you negate two conditions,  and Second :    not( a and b)   is not equivalent to  not a and not b

 

 

Ok, so what about a 3rd version of code. In Code Set C, we use or and not twice.

Look at the animation and truth table below and you’ll see that it works!!

It turns out that : 

 

 

Full Truth Table of DeMorgans Law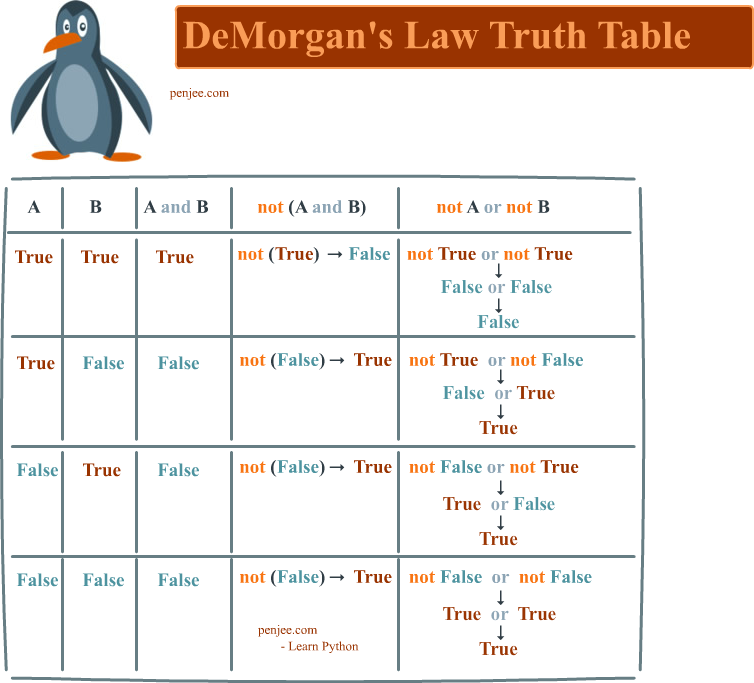

 

Summarizing It all

Python Code Example 1

is equivalent to

DeMorgan’s Law Truth Table

So, when you add the not you also must “flip” the and/or

Python Code Example 2

is equivalent to

Example 3

is equivalent to

Example 4

is equivalent to